树状数组

2021-08-09

如题目＞▽＜

简介

树状数组（Binary Index Tree, BIT），是一种简洁好用的数据结构，最简单的树状数组支持两种操作

单点修改：更改数组中某一个元素的值
区间查询：查询一个区间内所有元素的和
用途
可以解决大部分基于区间上的更新与求和问题
与线段树的区别
线段树是一个正经的二叉树，而树状数组会删去一定量的右枝，如果只用于区间求和，使用树状数组（代码短，少占空间）。如果在区间基础上实现更多的功能，则需要使用线段树
BIT的引入
对于普通数组，我们可以在$O(1)$的时间复杂度下修改元素，但区间求和则需要$O(n)$的复杂度

而对于前缀和数组，我们虽然可以在$O(1)$的时间复杂度下求区间长度，但由于修改元素会影响前缀和数组后面的元素，因此时间复杂度为$O(n)$

为了保证这两种操作的时间复杂度能均衡一点，我们便可以将数组分成若干个小区间进行维护，因此我们引入了BIT

树状数组巧妙运用了二进制，将区间以树的方式维护，形成一个新的数组，每个数组的元素值都是由当前元素下标值的二进制位减去该二进制位截取到最右面1后的数，直到为零。

设原数组$A$,当前下标为i，BIT为$C$，则$C_i+=A[i-lowbit(i)],i=i-lowbit(i)$,如下图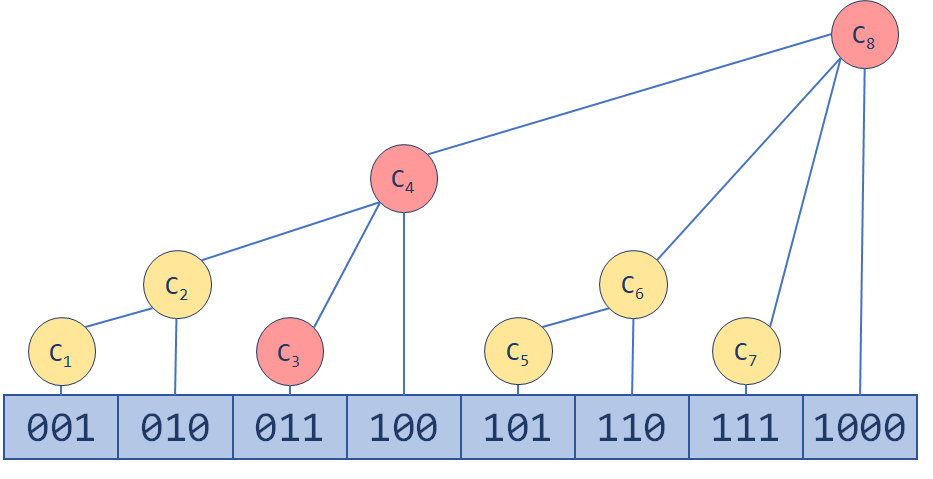

举个栗子：$C_4=A[100]+A[100-001]+A[11-01]+A[10-01]$

更新：相当于一个爬树的过程，向上更新，直到MAX(数组的容量)

求区间值:对$[a,b]$进行区间查询只需查询 $[1，b]$ 和 $[1,a]$ 然后相减即可

#lowbit

1	lowbit(x)=x&(-x)

为什么可以这样？我们需要知道，计算机里有符号数一般是以补码的形式存储的。-x相当于x按位取反再加1，会把结尾处原来1000…的形式，变成0111…，再变成1000…；而前面每一位都与原来相反。这时我们再把它和x按位与，得到的结果便是lowbit(x)。下面的图中举了两个例子：

int tree[MAXN];
inline void update(int i, int x)
{
    for (int pos = i; pos < MAXN; pos += lowbit(pos))
        tree[pos] += x;
}

inline int query(int n)
{
    int ans = 0;
    for (int pos = n; pos; pos -= lowbit(pos))
        ans += tree[pos];
    return ans;
}

inline int query(int a, int b)
{
    return query(b) - query(a - 1);
}

在初始化的时候，我们只需将每个点都update即可。

普通数组即可

见上述详解

我们可以引入一个差分数组b
设数组原数组为a，则有$b[i]=a[i]-a[i-1];(a[0]=0;)$，那么$a[i]=b[1]+….+b[i]$，求单点就是差分数组的前n项和，剩下都一样了

对于分块的区间查询，要注意块与块之间的重叠
计数问题

树状数组详解
 关于线段树(Segment tree)和树状数组(BIT)的区别？
算法学习笔记(2) : 树状数组