素数筛

2021-08-09

如题目＞▽＜

一、埃氏筛：

朴素的筛法叫埃氏筛（the Sieve ofEratosthenes，埃拉托色尼筛），它的过程是这样的：

我们把2~n的数按顺序写出来：

从前往后看，找到第一个未被划掉的数，2，这说明它是质数。然后把2的倍数（不包括2）划掉：

下一个未被划掉的数是3，它是质数，把3的倍数划掉：

接下来应该是5，但是5已经超过根号16了，所以遍历结束，剩下未被划掉的都是素数：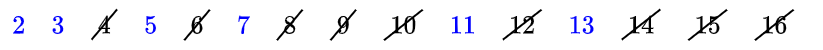

如何？是不是比一个一个判断快多了？这个过程写成代码就是：

bool isnp[MAXN]; // is not prime: 不是素数
void init(int n)
{
    for (int i = 2; i * i <= n; i++)
        if (!isnp[i])
            for (int j = i * i; j <= n; j += i)
                isnp[j] = 1;
}

代码也很简洁。这个算法的复杂度是 OnLOGLOGn ，还是非常优秀了。但是我们可能会发现，在筛的过程中我们会重复筛到同一个数，例如12同时被2和3筛到，30同时被2、3和5筛到。所以我们引入欧拉筛，也叫线性筛，可以在 O（n）时间内完成对2~n的筛选。它的核心思想是：让每一个合数被其最小质因数筛到。

二、欧拉筛
我们这次除了把2~n列出来，还维护一个质数表：

还是从头到尾遍历，第一个数是2，未被划掉，把它放进质数表：

然后我们用2去乘质数表里的每个数，划掉它们：

下一个是3，加入质数表，划掉6、9：

下一个是4（注意这里划掉的数也要遍历，只是不加入质数表），先划掉8，但我们不划掉12，因为12 （12=2x6=3x4）应该由它的最小质因数2筛掉，而不是3。

具体地说，如这里的2能整除4，则 4=2x2，那么对于任何大于2的质数p ，都有4p=2x2p ，其中2是一个比 p 更小的质数，所以 4p 应该被2筛掉而不是被p 筛掉。

下一个是5，加入质数表，划掉10，15：

下一个是6，划掉12，6被2整除，跳过。

……

按这样的步骤进行下去，可以筛掉所有的合数，并得到一张质数表。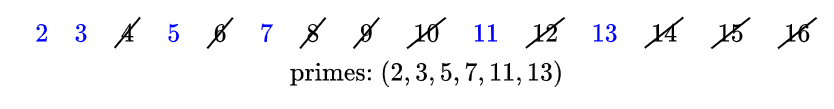

代码如下（C++11风格）：

bool isnp[MAXN];
vector<int> primes; // 质数表
void init(int n)
{
    for (int i = 2; i <= n; i++)
    {
        if (!isnp[i])//是质数就存入质数表
            primes.push_back(i);
        for (int p : primes)
        {
            if (p * i > n)
                break;
            isnp[p * i] = 1;//标记为合数
            if (i % p == 0)
                break;
        }
    }
}

(卡c++11版本)

bool isnp[P];
int primes[P]; // 质数表
int pos;
void init(int n)
{
    for (int i = 2; i <= n; i++)
    {
        if (!isnp[i])//是质数就存入质数表
            primes[pos++] = i;
        for (int j = 0; j < pos; j++)
        {
            int p = primes[j];
            if (p * i > n)
                break;
            isnp[p * i] = 1;//标记为合数
            if (i % p == 0)
                break;
        }
    }
}

(超短风格)

void get_prime(int n){//n是筛的范围，超1e8就不好使了
    for(int i = 2; i <= n; i ++){
        if(!isnp[i]) primes[cnt ++] = i;
        
        for(int j = 0; primes[j] <= n / i; j ++){
        //这里没对j限制，因为筛质数是以i*p[j]实现的
        //而当i*p[j]>n就该结束了，所以不用限制j
            isnp[primes[j] * i] = true;
            if(i % primes[j] == 0) break;
        //这里是欧拉筛的精髓
        //保证每个合数只被自己的最小质因子筛去
        //减少了重复筛的垃圾时间
        }
    }
}

注意判断越界那里最好使用乘法而不是除法，一般不会溢出，计算机算除法比乘法要慢得多。

欧拉筛除了解决一些卡埃氏筛的毒瘤题比如洛谷P3383，线性筛模板外，在后续一些数论算法中还有更多的应用。