本文对序列性动态规划经典例题进行讲解
序列型动态规划(从下标1开始计算)
1.题目:房屋染色
题意:
- 有一排N栋房子,每栋房子需要刷:红、蓝、绿其中一种颜色
- 任何两栋相邻房子不能刷成同一颜色
- 第i栋房子染成红、蓝、绿的花费分别是cost[i][0],cost[i][1],cost[i][2]
- 最少要花多少钱油漆这些房子
动态规划组成部分
1. 确定状态
- 最后一步:最优策略中房子N-1一定染成 红、蓝、绿中的一种,而N-2栋房子一定不能和第N-1栋颜色一样(上一步的钱数与颜色两种因素共同影响当前步),所以我们需要再开一维来表示房子的颜色
- 子问题:求出前N栋房子并且第N-1栋房子在红、蓝、绿颜色的最小花费
- 状态:设油漆前i栋房子,并且第i-1栋房子是红、蓝、绿的最小花费为f[i][0],f[i][1],f[i][2]
2. 转移方程
- $f[i][0]=min{f[i-1][1]+cost[i-1][0],f[i-1][2]+cost[i-1][0]}$
- $f[i][1]=min{f[i-1][0]+cost[i-1][1],f[i-1][2]+cost[i-1][1]}$
- $f[i][2]=min{f[i-1][0]+cost[i-1][2],f[i-1][3]+cost[i-1][2]}$
3. 初始条件和边界情况
- 初始条件:f[0][0]=f[0][1]=f[0][2]=0 前0个什么都没有
- 无边界情况
4. 程序
2.题目:房屋染色2
题意:
- 有一排N栋房子,每栋房子需要刷K种颜色的一种
- 任何两栋相邻房子不能刷成同一颜色
- 第i栋房子染成第j种颜色的花费是cost[i][j]
- 最少要花多少钱油漆这些房子
动态规划组成部分
1. 确定状态
- 最后一步:与第一题相似,还是最后一栋与前一栋颜色不能一样所以我们需要再开一维来表示房子的颜色
- 子问题:求出前N栋房子并且第N-1栋房子在K种颜色的最小花费
- 状态:设油漆前i栋房子,并且第i-1栋房子是1,2……K颜色的最小花费为f[i][0],f[i][1],f[i][2]……f[i][k-1]
2. 转移方程
- $f[i][j]=min_{k!=j}(f[i-1][k])+cost[i-1][j]$
3. 初始条件和边界情况
- 初始条件:f[0][0]=f[0][1]=f[0][2]=……=f[0][k-1]=0 前0个什么都没有
- 无边界情况
4.时间优化
在转移方程中,每次我们都需要在k不同于j颜色中找到$f[i-1][k]$的最小值,因此这块的时间复杂度为$O(k^2)$,我们可以将其优化到$O(k)$。我们可以不用每次都查找最小值,而是把最小值与次小值都记录下来
如果最小值是第i个元素,次小值是第j个元素
- 除掉的是第i个元素以外的元素,最小值就是第i个元素
- 除掉的是第i个元素,最小值就是第j个元素
3.题目:打家劫舍
题意:
- 有一排N栋房子,房子i里有A[i]个金币
- 魔理沙想选择一些房子偷金币
- 但是不能偷任何挨着的两家邻居,否则会被灵梦逮住
- 问她最多能偷多少金币
动态规划组成部分
1. 确定状态
- 最后一步:在最优的策略中,魔理沙需不需要偷最后一栋房子n
- 如果不偷,那么前n-1栋房子就是最优策略
- 如果偷,那么前n-2栋房子+偷第n栋房子就是最优策略
- 状态:设偷前i栋房子,前i栋房子最多能偷f[i]个金币
2. 转移方程
- $f[i]-max(f[i-1],f[i-2]+A[i-1])$
3. 初始条件和边界情况
- 初始条件:f[0]=0(没房子,偷个寂寞),f[1]=A[0]
- 无边界情况
3.题目:打家劫舍2
题意:
- 有一圈N栋房子,房子i里有A[i]个金币
- 魔理沙想选择一些房子偷金币
- 但是不能偷任何挨着的两家邻居,否则会被灵梦逮住
- 问她最多能头多少金币
和第一题几乎一致,收尾相接处判断如下:
由于第一个房子和最后一个房子不能同时偷所以我们可以将这一圈拆开 - 从第一个房子开始偷,偷到第N-1栋房子
- 从第二个房子开始偷,偷到第N栋房子
现在是炒股时间!!!
1.买卖股票的最佳时机
思路
记录当前位置前的最小值,当前价格减去最小价格就是当前能获得的最高利润,选出整个区间的最高利润即可
2.买卖股票的最佳时机2
思路
随便买入,那么我们只需要把所有涨的情况全买下来就妥了
3.买卖股票的最佳时机3
题意:
- 给定一支股票N天的价格
- 可以进行最多两次买+两次卖,每次都只买一股
- 不能在卖光手中股票前买入,但可以同一天卖完后买入
- 求最大收益
动态规划组成部分
1. 确定状态
- 最后一步:在最优的策略中,最后一次卖发生在第j天
- 枚举最后一次买在第i天
- 但我们不知道在第i天买是第几次,因此我们需要多加一个状态来表示是第几次买卖
- 记录阶段
- 不知道有没有买过,所以需要记录下来
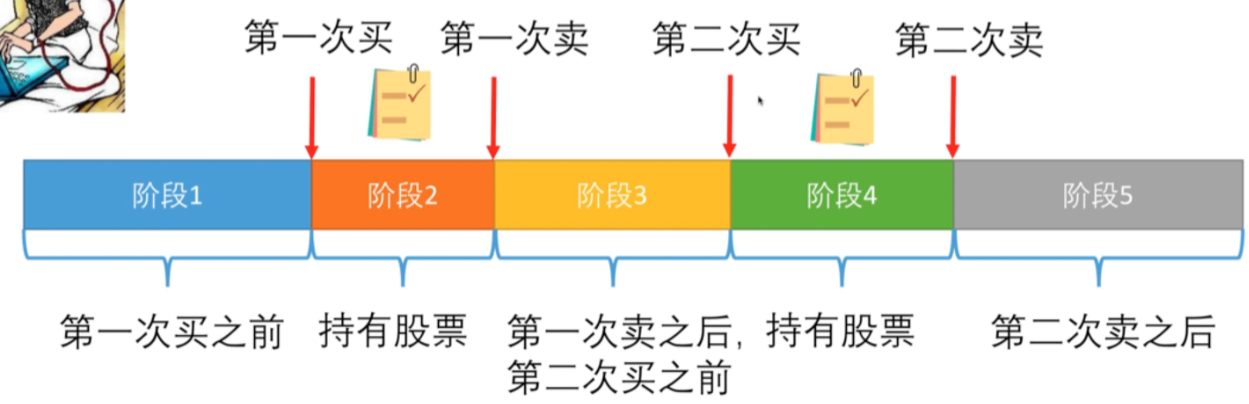
- 最优策略一定是前N天(第N-1天)结束后,处于
- 阶段1:没买卖过
- 阶段3:买卖过1次
- 阶段5:买卖过2次
- 状态:f[i][j],前i天(第i-1天)结束后,处在阶段j的最大获利
2. 转移方程
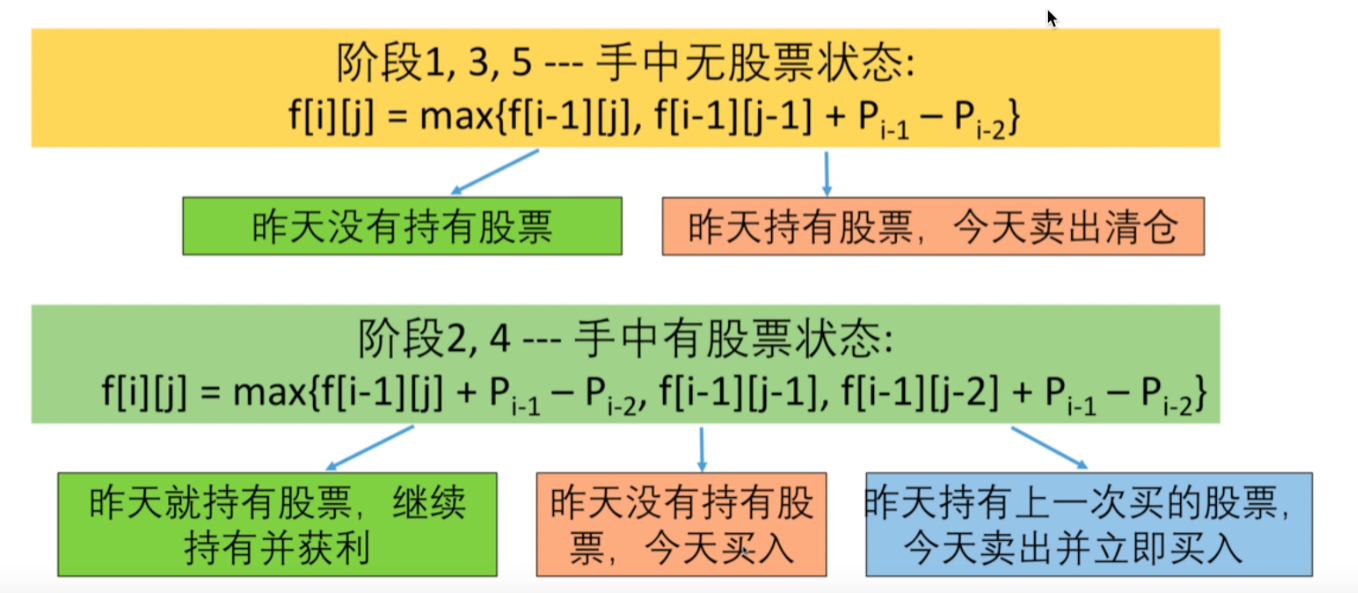
3. 初始条件和边界情况
- 初始条件:刚开始(前0天,属于阶段1)
- f[0][1]=0
- f[0][2]=f[0][3]=f[0][4]=f[0][5]=-inf
- 边界情况:如果 j-1<1 或 j-2<1 或 i-2<0,对应项不计入max(防止出现无意义的情况,下标越界)
3.买卖股票的最佳时机4
题意:
- 给定一支股票N天的价格
- 可以进行最多K次买+K次卖,每次都只买一股
- 不能在卖光手中股票前买入,但可以同一天卖完后买入
- 求最大收益
思路:
- 当k>n/2时,相当于可以无限买入卖出,和买卖股票2一样
- 对于一小段一小段连续的上升我们可以看成一整段的上升,而下降是一整段的下降
- 所以极限买入卖出就是每一段都是上升下降的波浪形////,这样的极限k就是n/2了
- 其余情况,便可参考买卖股票3,将k次买卖分成2*k+1段进行动态规划,就可以了
最长序列型动态规划
1.题目:最长递增子序列
题意:
- 给定一个数组,找出其中严格递增子序列的长度
动态规划组成部分
1. 确定状态
- 最后一步:最优策略中以a[j]结尾的子序列一定是最长的
- 子问题:本来求a[j]结尾的上升子序列,现在需要知道在它之前小于它的元素a[i]结尾的上升子序列
- 状态:设f[i]是以a[i]结尾的最长上升子序列的长度
2. 转移方程
- $f[j]=max(1,f[i]+1(a[i]<a[j]ANDi<j))$
3. 初始条件和边界情况
- 初始条件:无
- 边界情况:
a[i]<a[j]ANDi<j
总结(坐标型与序列型动态规划的区分)
二者可互通
- 如果第一项不需要空串向后生成,可以直接写出来dp,那么就可以用坐标型
- 如果不是很清楚第0个元素该怎么处理,那么选用序列型比较合适

