如题目>▽<
划分型动态规划
1. 题目:解码方法
题意:
- 有一段由A-Z组成的字母串被加密成数字串
- 加密方式:A->1,B->2,……Z->26
- 给定加密后的数字串S,问有多少种方式解密成字符串
动态规划组成部分
1. 确定状态:
- 最后一步:最后一个字母是最后一位数字还是最后两位数字转化成的
- 子问题: 设数字串长度为N,要 求前N个字符的解密方式数,需要知道前N-1和前N-2个字符的解密方式数
- 状态:设数字串S前i个数字解密成字母串有f[i]种方式
2. 转移方程
- $f[i]=f[i-1]{S[i]对应一个字母}+f[i-2]{S[i-1]S[i]对应一个字母}$
3. 初始条件和边界情况
- 初始条件:f[0]=1 空串有一种解密
- 边界情况:如果i=1,只看最后一位数字(没有两位数)
4. 程序
2. 题目:完全平方数
题意:
- 给一个正整数n
- 问最少用几个完全平方数组成n
动态规划组成部分
1. 确定状态:
- 最后一步:最后的数一定是由某个数的平方和与剩下的数组成
- 子问题: 要求组成i的最小平方数需要比较出i减去一个平方数后的数需要的最小平方数组合的个数
- 状态:设能够组成i的最少的完全平方数有f[i]个
2. 转移方程
- $f[i] = min_{1<=j*j<=i}(f[i - j * j])+1$
3. 初始条件和边界情况
- 初始条件:f[0] = 0
- 边界情况:无
4. 程序
3. 题目:分割回文串 II
题意:
- 给一个字符串s
- 问最少分成几个回文子串需要分割几次
动态规划组成部分
1. 确定状态:
- 最后一步:最优策略有最后一段回文串 S[j……N-1],
- 子问题: 求前N个字符S[0..N-1]最少分为几个回文串,需要知道S前j个字符[0..j-1]最少可以划分成几个回文串
- 状态:设S前i个字符[0..i-1]最少可以划分成f[i]个回文串
2. 转移方程
- $f[i] = min_{0<=j<=i-1}(f[j]+1,S[j..i-1]是回文串)$
3. 初始条件和边界情况
- 初始条件:f[0] = 0 ,空串被分成0个回文串(序列型)
- 边界情况:无
4. 程序
4. 题目:书籍复印
题意:
- 有N本书待抄写,第i本书有A[i]页
- 有k个抄写员,每个抄写员可以抄写连续的若干本书(每分钟抄一页)
- 最少需要多长的时间抄完所有的书
动态规划组成部分
1. 确定状态:
- 最后一步:最后一个抄写员(第k个)抄写第j本到第N-1本书需要时间最短
- 子问题: 求K个人最短多长时间抄完前N本书,需要知道K-1个人最少多长时间抄完前j本书
- 状态:设f[k][i]为k个抄写员需要多长时间抄完前i本书
2. 转移方程
- $f[k][i] = min_{j=0..i}max(f[k-1][j],A[j] +..+ A[i-1])$
3. 初始条件和边界情况
- 初始条件:
- f[0][0] = 0 零个抄写员抄0本书。f[0][1]..f[0][N] = +inf
- f[k][0] = 0 每个抄写员花费0分钟抄0本书
- 边界情况:k > N ,可以赋值 k = N
4. 动态规划程序
二分查找程序小结
- 要求将一个序列或字符串划分成若干满足要求的片段
- 解决方法:最后一步->最后一段
- 枚举最后一段的起点
- 如果题目不指定段数,f[i]表示前i个元素分段后的可行性/最值:解码方法,完全平方数,分割回文串2
- 如果题目指定段数,用f[i][j]表示前i个元素分成j段或前j个元素分成i段后的可行性/最值:书籍复印
博弈型动态规划(规模不大)
1. 题目:硬币排成线
题意:
- 给N个物品,重量都是正整数
- 一个背包最大承重为M
- 最多能带走多重的物品
动态规划组成部分
1. 确定状态:
- 第一步:在当前局面走出一步可以让对手陷入必败的局面则必胜,在当前局面无路可走则必败
- 子问题:面对N个石子是否先手必胜,需要知道面对N - 1, N - 2个石子,是否先手必胜
- 状态:设f[i]为面对i个石子是否先手必胜
2. 转移方程
- $f[i] = f[i-1] == false OR f[i-2] == false$
3. 初始条件和边界情况
- 初始条件:f[0] = false 面对0个石子先手必输,f[1] = f[2] = true面对1,2个石子,先手必胜
4. 程序
背包问题
1. 题目:背包问题(可行性)
题意:
- 有n个物品装入背包,重量均为正整数
- 假设背包最多能承重m,最多能装多满
动态规划组成部分
1. 确定状态:
- 最后一个物品(重量$A_{N-1}$)是否放入背包
- 情况1:如果前N-1个物品能拼出W,当然前N个物品也能拼出W
- 情况2:如果前N-1个物品能拼出$W-A_{N-1}$,再加上最后的物品$A_{N-1}$,拼出W
- 子问题:要求前N个物品能否拼出重量0,1…,M,需要知道前N-1个物品能否拼出重量0,1,…,M
- 状态:设f[i][w]为能否用前i个物品拼出w
- 注意:背包问题一定要把承重放入状态
2. 转移方程
- $f[i][w] = f[i-1][w] OR f[i-1][w-A[i-1]]$
3. 初始条件和边界情况
- 初始条件:f[0][0]=true 前0个物品可以拼出重量0
- f[0][1..M]=false 0个物品拼不出大于0的重量
- 边界情况:f[i-1][w-A[i-1]]只能在w>=A[i-1]时使用
4. 程序
2. 题目:背包问题5(计数型)
题意:
- 有n个正整数,一个正整数Target
- 每个正整数只能用一次,求有多少种组合加起来是Target
动态规划组成部分
1. 确定状态:
- 最后一个物品(重量$A_{N-1}$)是否放入背包
- 情况1:如果前N-1个物品能拼出W,当然前N个物品也能拼出W
- 情况2:如果前N-1个物品能拼出$W-A_{N-1}$,再加上最后的物品$A_{N-1}$,拼出W
- 情况1的方式数+情况2的方式数=用前N个物品拼出W的方式数
- 子问题:要求前N个物品能否拼出重量0,1…,,需要知道前N-1个物品能否拼出重量0,1,…,Target
- 状态:设f[i][w]为用前i个物品多少种方式拼出w
- 注意:背包问题一定要把承重放入状态
2. 转移方程
- $f[i][w] = f[i-1][w] + f[i-1][w-A[i-1]]$
3. 初始条件和边界情况
- 初始条件:f[0][0]=1 前0个物品可以有一种方式拼出重量0
- f[0][1..M]=0 0个物品拼不出大于0的重量
- 边界情况:f[i-1][w-A[i-1]]只能在w>=A[i-1]时使用
4. 空间优化
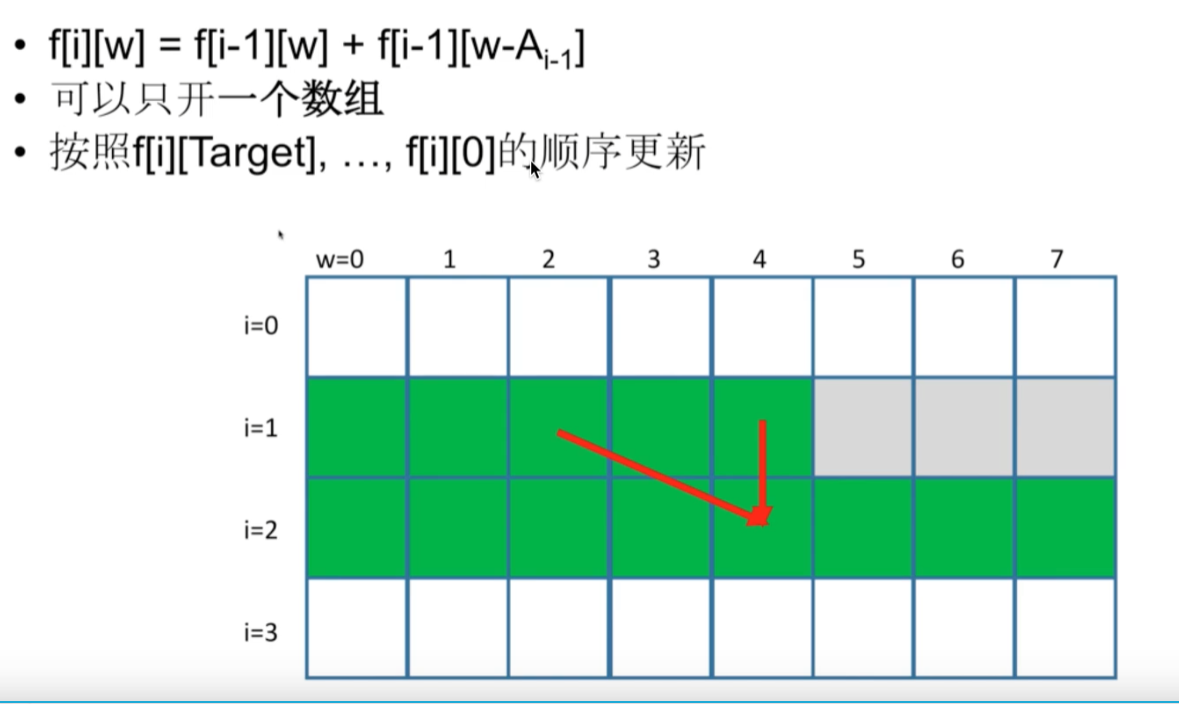
5. 程序
空间优化过的程序
3. 题目:背包问题2(最值型)
题意:
- 有n个物品,每个物品都有重量和价值两个属性
- 一个背包最大承重是正整数M
- 最多能带走多大价值的物品
动态规划组成部分
1. 确定状态:
- 最后一个物品(重量$A_{N-1}$价值$V_{N-1}$)是否放入背包
- 情况1:如果前N-1个物品能拼出W,最大总价值是V当然前N个物品也能拼出W并且总价值是V
- 情况2:如果前N-1个物品能拼出$W-A_{N-1}$最大总价值是V,再加上最后的物品(重量$A_{N-1}$价值$V_{N-1}$),拼出W,总价值为$V + V_{N-1}$
- 情况1的方式数+情况2的方式数=用前N个物品拼出W的方式数
- 子问题:要求前N个物品能否拼出重量0,1…,M,以及拼出重量W能获得的最大价值,需要知道前N-1个物品能否拼出重量0,1,…M,以及拼出重量W能获得的最大价值
- 状态:设f[i][w]为用前i个物品拼出w时获得的最大价值(-1表示无法拼出)
- 注意:背包问题一定要把承重放入状态
2. 转移方程
- $f[i][w] = max(f[i-1][w], f[i-1][w-A[i-1]] + V[i-1] |w >= A[i-1] AND f[i-1][w-A[i-1]] != -1)$
3. 初始条件和边界情况
- 初始条件:f[0][0]=0 前0个物品可以有一种方式拼出重量0,价值为0
- f[0][1..M]=-1 0个物品拼不出大于0的重量
- 边界情况:f[i-1][w-A[i-1]]只能在w>=A[i-1]时使用
4. 程序
空间优化过的程序
4. 题目:背包问题3(最值型)
题意:
- 有n种物品,每种物品都有重量和价值两个属性
- 每种物品都有无穷多个
- 一个背包最大承重是正整数M
- 最多能带走多大价值的物品
动态规划组成部分
1. 确定状态:
- 与背包2几乎一致,区别在于每次可以将一个物品放多次
- 状态:设f[i][w]为用前i个物品拼出w时获得的最大价值(-1表示无法拼出)
- 注意:背包问题一定要把承重放入状态
2. 转移方程
- $f[i][w] = max(f[i-1][w], f[i-1][w-kA[i-1]] + kV[i-1] |kw >= A[i-1] AND f[i-1][w-kA[i-1]] != -1)$
- 优化:f[i][w] = max(f[i-1][w], f[i][w-A[i-1]] + V[i-1] |w >= A[i-1] AND f[i-1][w-A[i-1]] != -1)$
3. 初始条件和边界情况
- 初始条件:f[0][0]=0 前0个物品可以有一种方式拼出重量0,价值为0
- f[0][1..M]=-1 0个物品拼不出大于0的重量
- 边界情况:f[i-1][w-A[i-1]]只能在w>=A[i-1]时使用
4. 空间优化
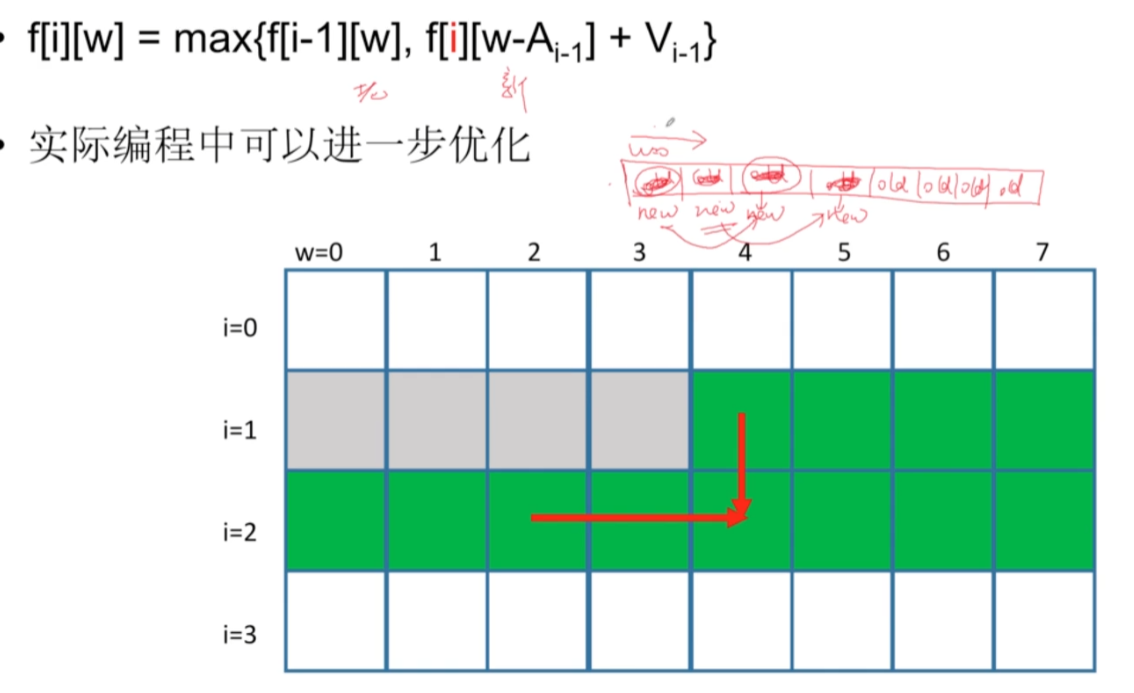
5. 程序
空间优化过的程序小结
- 可行性背包
- 题面:要求不超过Target时能拼出的最大重量
- 记录f[i][w]=前i个物品能否拼出重量w
- 计数型背包
- 题面:要求有多少种方式拼出重量Target
- 记录f[i][w]=前i个物品有多少种方式拼出重量w
- 最值型背包
- 题面:要求能拼出的最大价值
- 记录f[i][w]=前i个物品能拼出重量w能获得的最大价值
- 关键点
- 最后一步
- 最后一个背包里的物品是哪一个
- 最后一个物品有没有放进背包
- 数组大小和最大承重Target有关
- 最后一步

