动态规划-从建表到切题(4)

如题目＞▽＜

区间型动态规划

1. 题目：最长回文子串

题意：

• 一个字符串S,长度为N
• 找到它最长的回文子序列的长度

  动态规划组成部分

  1. 确定状态：

• 子问题：要求S[i..j]的最长回文子串
• 若S[i]=S[j],需要知道S[i+1..j-1]的最长回文子串(两边的字符相等)
• 否则答案是S[i+1..j]或S[i..j-1]的最长回文子串(两边的字符不等)
• 状态：设f[i][j]为S[i..j]的最长回文子串长度

  2. 转移方程

• $f[i][j] = max(f[i+1][j],f[i][j-1],f[i+1][j-1]+2 | s[i]=s[j])$

  3. 初始条件和边界情况

• 初始条件：f[0][0]=f[1][1]=…=f[n-1][n-1]=1(一个字母为长度为1的回文子串)
• 如果s[i]==s[i+1],f[i][i+1]=2
• 如果s[i]!=s[i+1],f[i][i+1]=1

  4. 计算顺序

  按照长度j-i，从小到大计算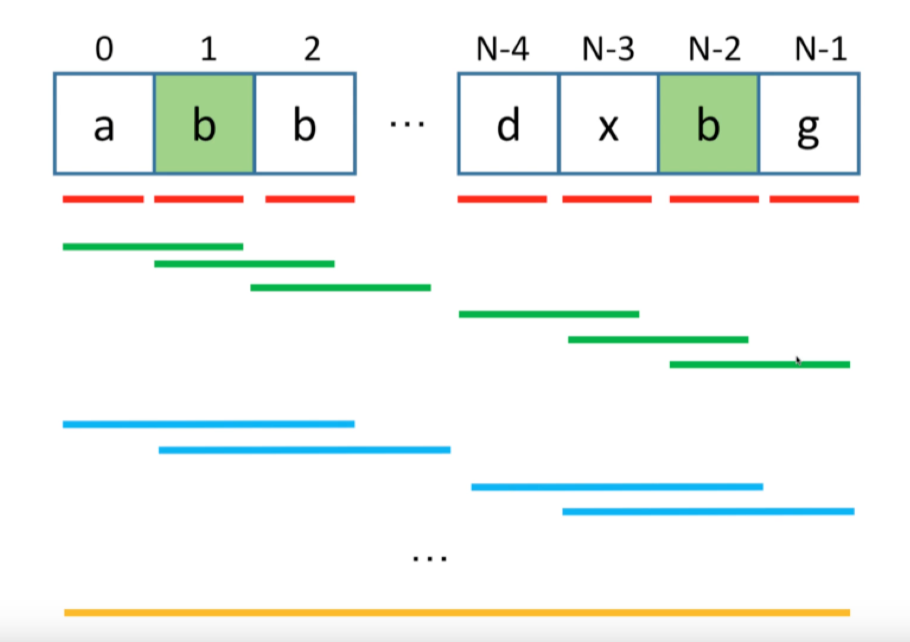
  

  5. 程序

---

2. 题目：完全平方数

题意：

• 给一个正整数n
• 问最少用几个完全平方数组成n

  动态规划组成部分

  1. 确定状态：

• 最后一步：最后的数一定是由某个数的平方和与剩下的数组成
• 子问题： 要求组成i的最小平方数需要比较出i减去一个平方数后的数需要的最小平方数组合的个数
• 状态：设能够组成i的最少的完全平方数有f[i]个

  2. 转移方程

• $f[i] = min_{1<=j*j<=i}(f[i - j * j])+1$

  3. 初始条件和边界情况

• 初始条件：f[0] = 0
• 边界情况：无

  4. 程序

赏

来根小鱼干好吗o( =·ω·= )m

支付宝

微信