堆排序

2021-09-22

如题目＞▽＜

堆排序，顾名思义，是利用堆的特性来进行排序。本文讲述利用大顶堆来进行非递减排序，非递增排序同理。

调整堆（heapify）

将某一个节点进行heapify操作，使得该节点（父亲节点）的值大于两个儿子节点，我们要保证交换后的子节点仍然是一个堆，所以同样需要以这个子节点为父节点继续进行heapify操作，直到进行到堆的最底部

因为完全二叉树的特性，在知道某一个点的下标的情况下，我们可以轻易地算出其父节点及其子节点的下标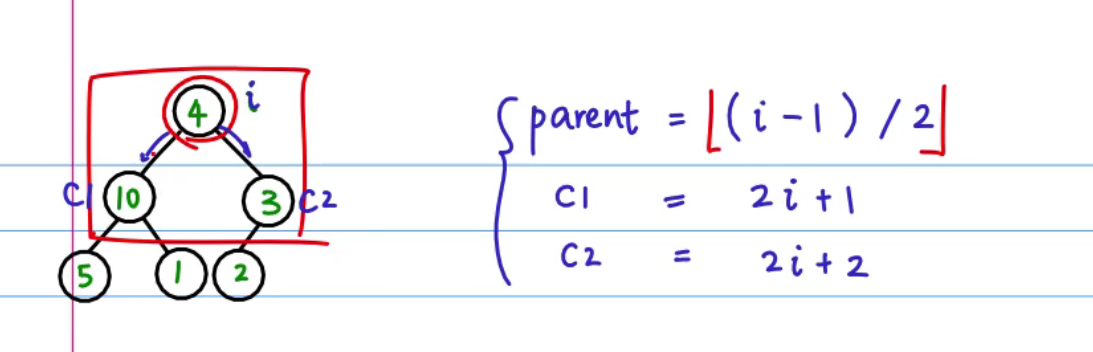

函数代码如下：

void heapify(int tree[], int n, int i) {
    if (i >= n) {
        return;
    }
    int c1 = 2 * i + 1;// 左孩子
    int c2 = 2 * i + 2;// 右孩子
    int max = i; // 记录最大值的下标
    
    if (c1 < n && tree[c1] > tree[max]) {
        max = c1;
    }
    if (c2 < n && tree[c2] > tree[max]) {
        max = c2;
    }

    if (max != i) {
        swap(tree[max], tree[i]);// 交换值，比较简单这里不给出具体写法
        heapify(tree, n, max);// 使交换后的节点仍满足父节点的值大于子节点的值，继续递归
    }
}

建立堆

对于一个乱序的数组，为了将其创建成一个堆，我们需要从最后一个父节点开始，层层向上进行heapify操作，这样我们就能保证所有的父节点均大于子节点，也就建立成了大顶堆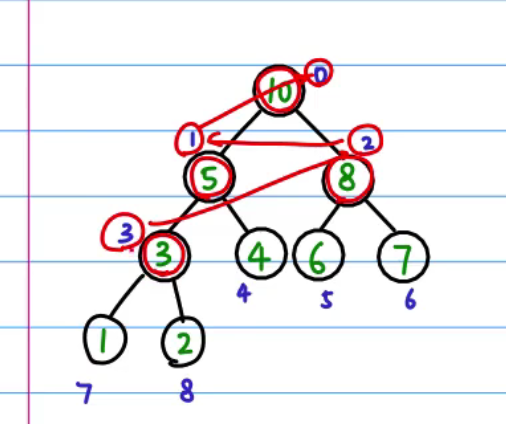

函数代码如下：

void build_heap(int tree[], int n) {
    int last_node = n - 1;// 最后一个节点的下标
    int parent = (last_node - 1) / 2;// 求出最后一个节点的父节点，也就是最后一个父节点
    for (int i = parent; i >= 0; i--) {
        heapify(tree, n, i);
    }
}

进入正戏！堆排序

现在我们已经建立出了大顶堆，我们此时可以将堆顶与堆底的最后一个元素交换。这样，我们就将最大的数排好序了。对于新交换来的点，为了继续维护大顶堆，我们仍需要进行heapify的操作，不过此时的n应该变为n-1（因为我们已经将最后的元素排好序了）。
函数代码如下：

void heap_sort(int tree[], int n) {
    build_heap(tree, n);

    for (int i = n - 1; i >= 0; i--) {
        swap(tree[0], tree[i]);
        heapify(tree, i, 0);// 最后一个最大值点已经排好，长度要减一进行heapify操作
    }
}

例题,快速排序