八大排序

2023-08-25

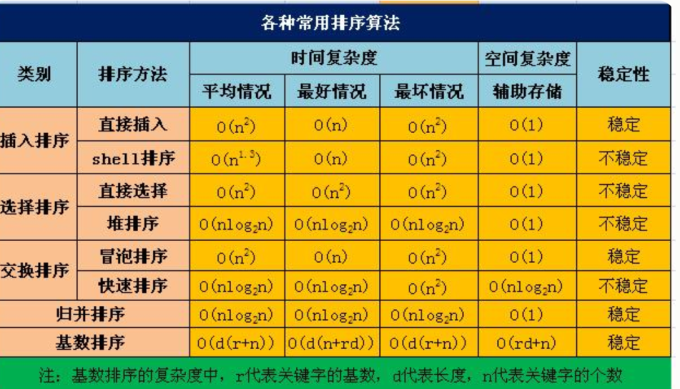
经典的八种排序算法

如题目＞▽＜

直接插入排序

将数组中的所有元素依次跟前面已经排好的元素相比较，如果选择的元素比已排序的元素小，则交换，直到全部元素都比较过。

代码

for(int i=1;i<n;i++){ //从第2个数开始，取出当前数作为待排序数
int j, tmp = a[i];
    for (j = i; j >= 0; j--) {
        if (a[j] < tmp) {// 待排的数刚好比指向的数大时结束
            break;
        }
    }
    for (int k = i;k > j+1;k--) {// 较小的数位置是j，j+1是要插入的位置，所以需要从j+1位后把前一位移过来。
        a[k]=a[k-1];
    }
    a[j+1] = tmp;// j+1为待插入的位置
}

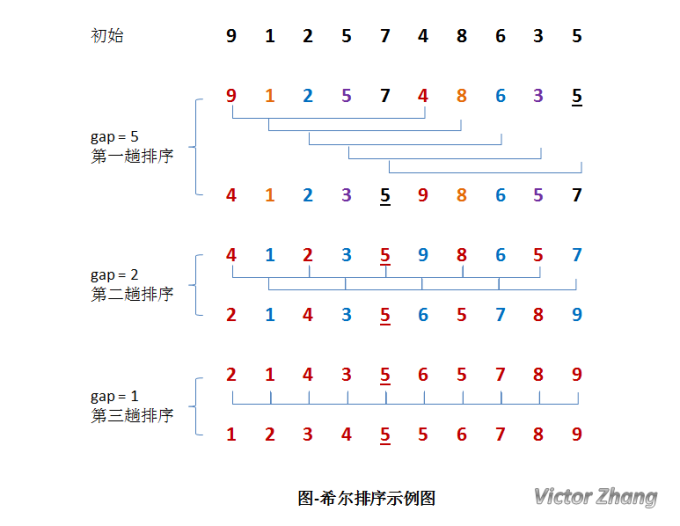
希尔排序

希尔排序的算法思想：将待排序数组按照步长gap进行分组，然后将每组的元素利用直接插入排序的方法进行排序；每次将gap折半减小，循环上述操作；当gap=1时，利用直接插入，完成排序。
同样的：从上面的描述中我们可以发现：希尔排序的总体实现应该由三个循环完成：

第一层循环：将gap依次折半，对序列进行分组，直到gap=1

第二、三层循环：也即直接插入排序所需要的两次循环。具体描述见上

代码

// 由于序列近似有序时插入排序时间复杂度很低，因此可以用增量的方法，使序列基本有序
for(int dk = n / 2; dk >= 1; dk = dk / 2){// 增量变化（折半）
    for(int i = dk; i < n; i++) {// 此时保持在中轴偏右的位置
        if (a[i] < a[i - dk]) {// 排好的顺序是左小右大，当前待排的数比前面那个小时才需要放到前面排序
            int j, tmp = a[i];// 暂存待排值
            for (j = i - dk; j >= 0 && a[j] > tmp; j-= dk) {
                a[j + dk] = a[j];//记录后移，因此需要j>=0使j后的记录全部后移，腾出j的位置，以供新元素插入
            }
            a[j+dk] = tmp;// for循环结束会多减去个1，要加上
        }
    }
}

选择排序

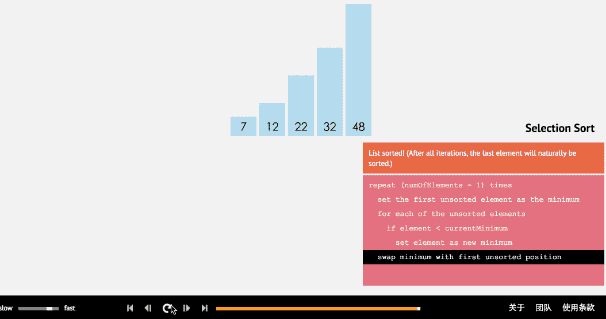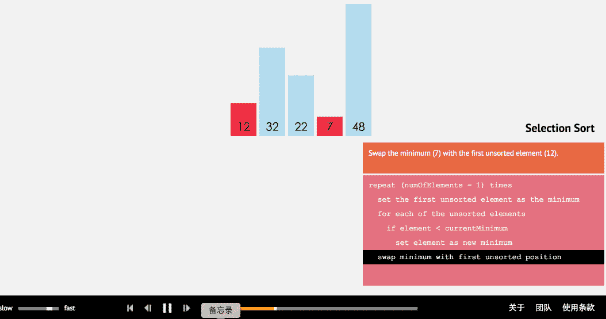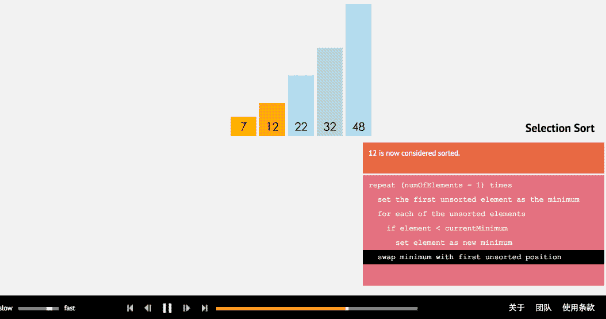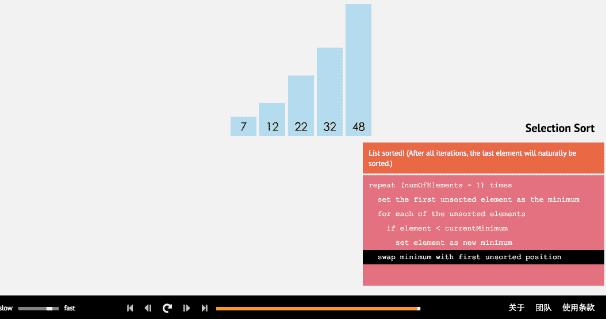
简单选择排序的基本思想：比较+交换。

从待排序序列中，找到关键字最小的元素；
如果最小元素不是待排序序列的第一个元素，将其和第一个元素互换；
从余下的 N - 1 个元素中，找出关键字最小的元素，重复(1)、(2)步，直到排序结束。
因此我们可以发现，简单选择排序也是通过两层循环实现。
第一层循环：依次遍历序列当中的每一个元素
第二层循环：将遍历得到的当前元素依次与余下的元素进行比较，符合最小元素的条件，则交换。

代码

for (int i = 0; i < n; i++) {
    int minn = i;// 最小元素的下标
    for (int j = i+1; j < n; j++) {// 从排好序的下一个开始查找
        if (a[j] < a[minn]) {// 持续更新最小元素的下标
            minn = j;
        }
    }
    swap(a[i], a[minn]);
}

堆排序

堆排序，顾名思义，是利用堆的特性来进行排序。本文讲述利用大顶堆来进行非递减排序，非递增排序同理。

调整堆（heapify）

将某一个节点进行heapify操作，使得该节点（父亲节点）的值大于两个儿子节点，我们要保证交换后的子节点仍然是一个堆，所以同样需要以这个子节点为父节点继续进行heapify（调整堆）操作，直到进行到堆的最底部

因为完全二叉树的特性，在知道某一个点的下标的情况下，我们可以轻易地算出其父节点及其子节点的下标

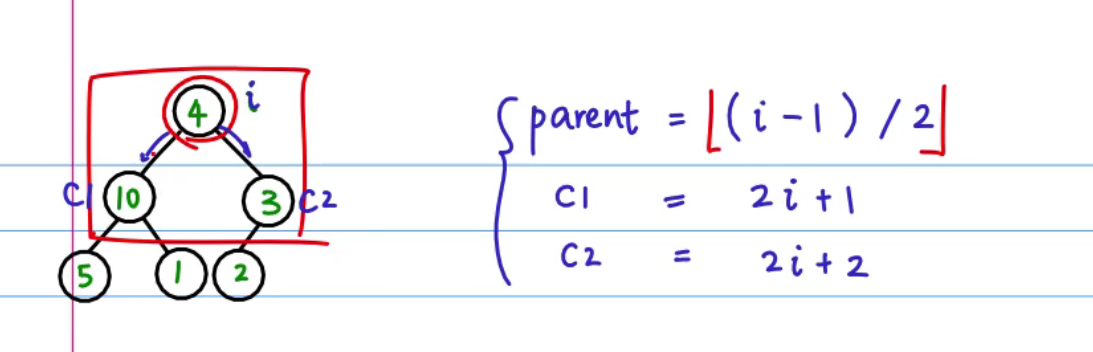
函数代码如下：

// n:堆的大小 i：待调整的元素下标
void heapify(int tree[], int n, int i) {
    if (i >= n) {
        return;
    }
    int c1 = 2 * i + 1;// 左孩子
    int c2 = 2 * i + 2;// 右孩子
    int max = i; // 记录最大值的下标
    
    if (c1 < n && tree[c1] > tree[max]) {
        max = c1;
    }
    if (c2 < n && tree[c2] > tree[max]) {
        max = c2;
    }

    if (max != i) {
        swap(tree[max], tree[i]);// 交换值，比较简单这里不给出具体写法
        heapify(tree, n, max);// 使交换后的节点仍满足父节点的值大于子节点的值，继续递归
    }
}

建立堆

对于一个乱序的数组，为了将其创建成一个堆，我们需要从最后一个父节点开始，层层向上进行heapify操作，这样我们就能保证所有的父节点均大于子节点，也就建立成了大顶堆

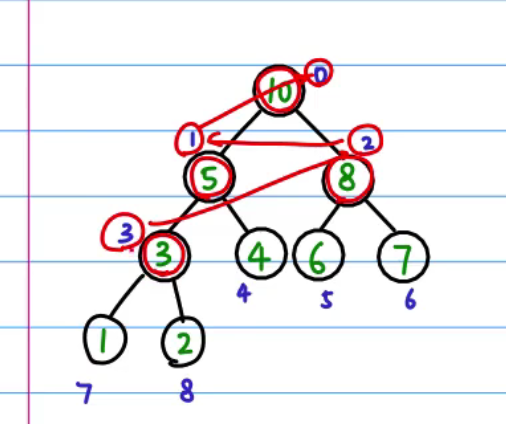
函数代码如下：

void build_heap(int tree[], int n) {
    int last_node = n - 1;// 最后一个节点的下标
    int parent = (last_node - 1) / 2;// 求出最后一个节点的父节点，也就是最后一个父节点
    for (int i = parent; i >= 0; i--) {
        heapify(tree, n, i);
    }
}

进入正戏！堆排序

现在我们已经建立出了大顶堆，我们此时可以将堆顶与堆底的最后一个元素交换。这样，我们就将最大的数排好序了。对于新交换来的点，为了继续维护大顶堆，我们仍需要进行heapify的操作，不过此时的n应该变为n-1（因为我们已经将最后的元素排好序了）。
函数代码如下：

void heap_sort(int tree[], int n) {
    build_heap(tree, n);

    for (int i = n - 1; i >= 0; i--) {
        swap(tree[0], tree[i]);
        heapify(tree, i, 0);// 最后一个最大值点已经排好，长度要减一进行heapify操作
    }
}

例题,快速排序

冒泡排序

代码

// 不解释
for (int i = 0; i < n; i++) {
    for (int j = i + 1 ; j < n; j++) {
        if (a[i] > a[j]) {
            swap(a[i], a[j]);
        }
    }
}

快速排序

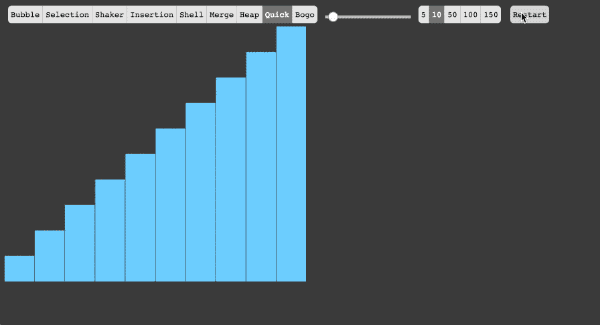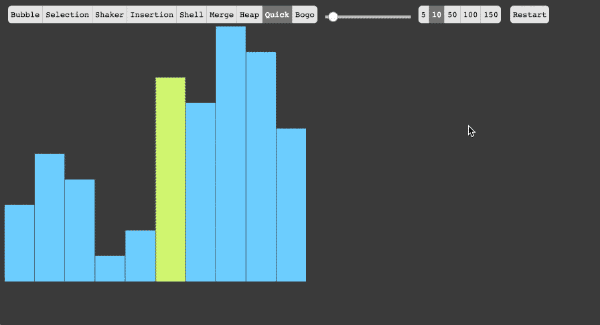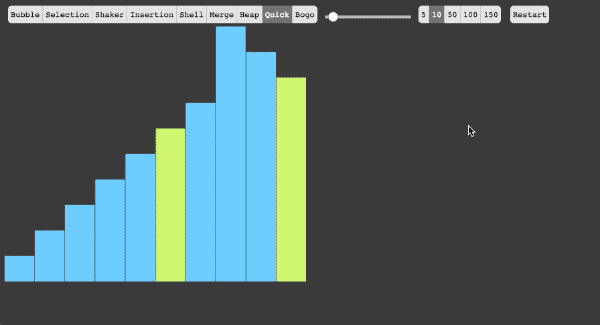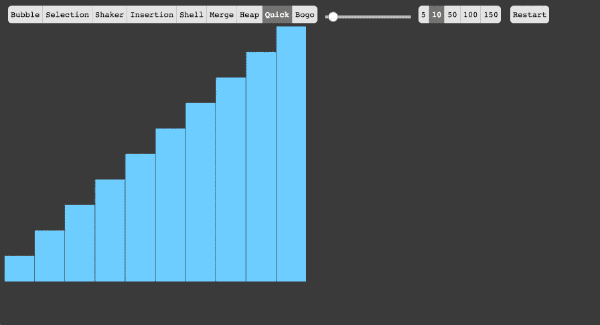
从序列当中选择一个基准数(pivot)
在这里我们选择序列当中第一个数最为基准数（教材就是这个基准数）
将序列当中的所有数依次遍历，比基准数大的位于其右侧，比基准数小的位于其左侧
重复步骤1.2，直到所有子集当中只有一个元素为止。
用伪代码描述如下：

i = L; j = R; 将基准数挖出形成第一个坑a[i]。
j–由后向前找比它小的数，找到后挖出此数填前一个坑a[i]中。
i++由前向后找比它大的数，找到后也挖出此数填到前一个坑a[j]中。
再重复执行2，3二步，直到i==j，将基准数填入a[i]中

代码

void quick_sort(int low, int high) {
    int i = low;
    int j = high;
    if (i >= j) {// 当前序列长度为1或0时，直接返回
        return;
    }
    // srand(time(0));
    // swap(a[i], a[rand() % (j - i + 1) + i]);// 随机基准数，能更好应对原序列大致有序的情况
    int tar = a[i]; // 第一个数为基准数
    while (i < j) {
        while (i < j && a[j] >= tar) {// 哨兵j先向左查找比基准数小的数
            j--;
        }
        if (i < j)
            a[i++] = a[j];// 先赋值再自增
        while (i < j && a[i] < tar) {// 哨兵i再向右查找比基准数大的数
            i++;
        }
        if (i < j)
            a[j--] = a[i];// 先赋值再自减
    }
    a[i] = tar;
    quick_sort(low, i - 1);// 左半边序列
    quick_sort(i+1, high);// 右半边序列
}

归并排序

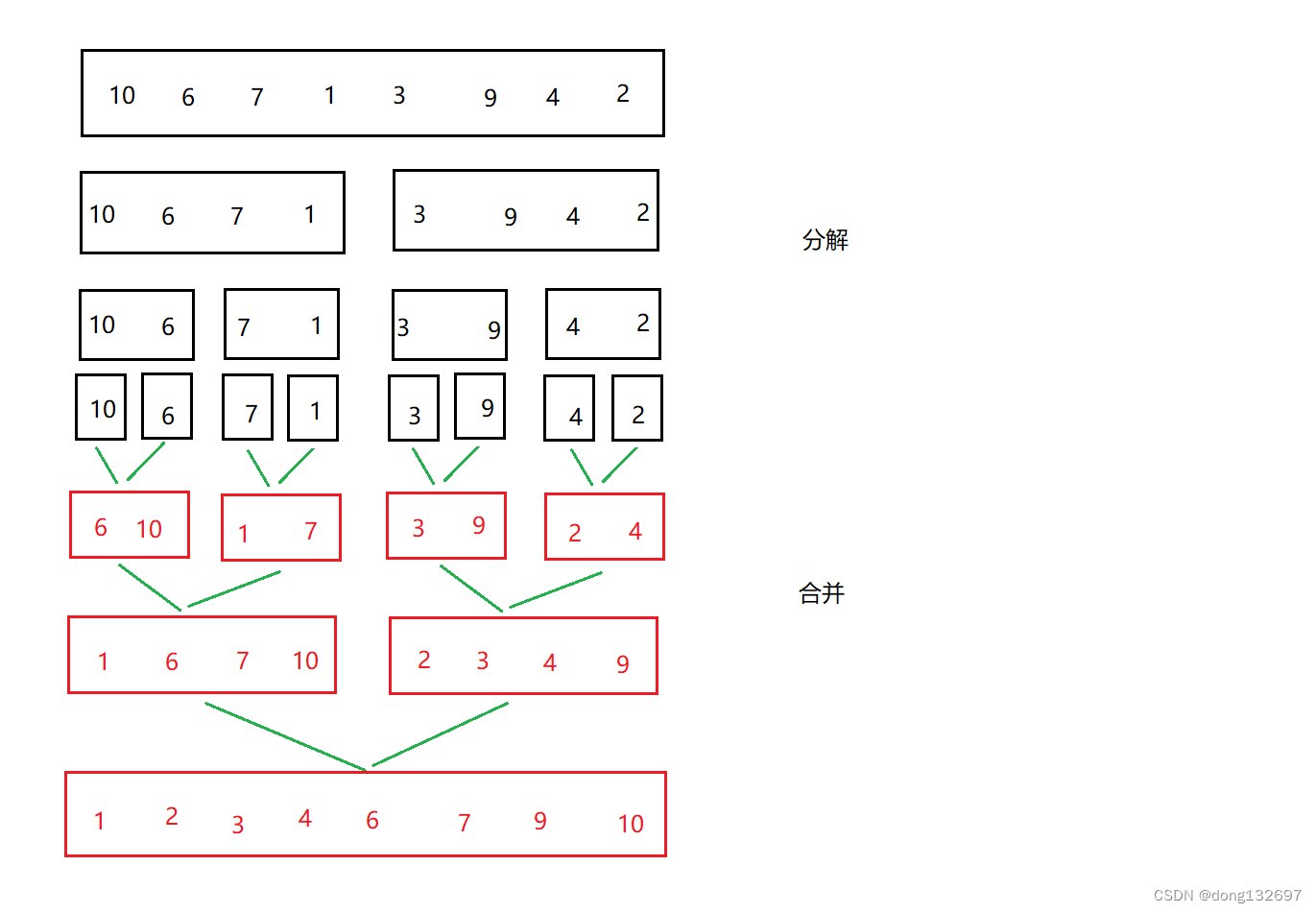
归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。
所谓归并，就是将两组有序的数据合成为一组有序的数据，例如有如下两个有序数组，将两个有序数组归并为一个有序数组，这就是一次归并操作。

代码

int a[MAX], b[MAX];
ll res;
void merge_sort(int l, int r) {
	if (l == r) return;
	int mid = (l + r) / 2;
	merge_sort(l, mid);
	merge_sort(mid+1, r);
	int k = l, i = l, j = mid+1;
	while(i <= mid && j <= r){
		if (a[i] <= a[j]) {
			b[k++] = a[i++];
		} else {
			b[k++] = a[j++];
			res += mid - i + 1;// 可以顺带求逆序对
		}
	}
	while (i <= mid) {
		b[k++] = a[i++];
	}
	while (j <= r) {
		b[k++] = a[j++];
	}
	for (int i = l; i <= r; i++) {
		a[i] = b[i];
	}
}